gekrümmte Kurven
Der Canon Gubernauticus des John Dee "lebt" gewissermaßen davon, daß spätestens seit Pedro Nunes und der so großartigen Darstellung der "paradoxen Kompaßkurven" durch Gerhard Mercator diese Kurven als spiralig-gekrümmt ausgemacht worden sind.
Dabei waren mindestens Nunes und Dee - dem schon in jungen Jahren "unendlich" Belesenen - bekannt, daß sich die "Alten" längst mit spiralig-krummen Linien, die wir heute "spirig" nennen, beschäftigt hatten: So hatte sich um 130 vChr schon Perseus mit den ebenen Schnitten eines Torus ( griech. spetra, Kreiswulst) beschäftigt und drei ihrer Hauptformen "Spiralen" genannt. Ebenso beschäftigten sich Archytas von Tarent und Eudoxus von Knidos mit dem Torus, der bekanntlich entsteht, wenn man einen Kreis sich um eine Gerade seiner Ebene gleichförmig herum"winden" läßt. Einige der "krummen Linien" des Altertum sind verloren gegangen, so z.B. der "Kochlias", die Hausschnecke des Apollonius, deren Projektion auf die Ebene einer logarithmischen Spirale sehr ähnlich sieht. Und Demetrius von Alexandrien, Philo von Tyana und auch Menelaus haben über "paradoxe Linien" geschrieben, die vermutlich der logarithmischen Spirale ähnlich gewesen sind. (Vgl. Moritz Cantor: Vorlesungen über die Geschichte der Mathematik2, 1894-1901, 3 Bde, hier I 296, 350.)

Hat John Dee von diesen "paradoxen" zweifach-krummen Kurven gewußt? Ein Leichtes wäre es dann gewesen, von der doppelt-gekrümmten Linie des Kompaßkurses als einem "paradoxem Kompaß(kurs)" zu sprechen. 

schreibt
The Haven-Finding Art: A History of Navigation from Odysseus to Captain Cook
London 1956, 197: "John Dee, unfortunately, preferred to keep his specialized knowledge out of print, and it is impossible to tell quite what his new instrument was which he called the Paradoxall Compass, and taught the use of to the Boroughs. It was not, of course, a mariners' compass, but appears to have included a polar zenithal chart for setting course and avoiding the errors of the plain chart."
Charlotte Fell: John Dee, London 1909. Ch.Fell schreibt S.31: "He [Dee] had spent most of the previous year (1576) in writing a series of volumes to be entitled 'General and Rare Memorials pertayning to the perfect art of Navigation.' The first volume, The British Monarchy, or Hexameron Brytannicum, was finished in August. It was dedicated to Christopher Hatton ... [Sir Christopher Hatton hatte er zum Sponsor des zweiten Buches erkoren - daher wohl die Widmung - : aber die Druckkosten waren einfach zu hoch.]  The second volume, The British Complement, 'larger in bulk than the English Bible', was written in the next four months and finished in December. It was never published; its author tells us it would cost many hundreds of pounds to print, because of the tables and figures requisite, and he must first have a 'comfortable and sufficient opportunity or supply thereto.' The necessary funds were never forthcoming, and the book remained in manuscript. A considerable part of it is devoted to an exposition of the 'paradoxall' compass which its author had invented in 1557." S.120 : "A couple of globes of Gerard Mercator’s best make were among the most valuable contents of the library, especially as upon the celestial globe Dee had marked his own observations of comets, their place and path in the heavens. There were other objects which Mercator had constructed specially for Dee, vis., three theorics [?annuli astronomici], two with horizon and meridian lines in copper. A number of compasses of many kinds were among the objects, for Dee had invented, as we have seen, what he calls a 'Paradoxall Cumpass.' There was also a great piece of load-stone, or 'magnes-stone', of extraordinary virtue. It had been sold for five shillings, but 'being divided up and parted with piece-meal it made more than 20 pounds'.”

1999 fand ich in der "Calder Thesis" - veröffentlicht von der John-Dee-Gesellschaft - im WWW.johndee.org/calder/html/Calder7.html, Kapitel VII.V, den folgenden Text, der das seinerzeitige Nicht-Wissen über den Paradoxen Kompaß in Abhängigkeit von Frau Taylor beschreibt (alle Hervorhebungen von  mir):

"Dee was particularly concerned with promoting the development of navigation and discovery; he refers frequently to two inventions he has made, which he considered important contributions to progress in this field — his "Paradoxall Compass" and Compass of Variation.
There is evidence of Dee's longstanding interest in the magnet — he used it as an example in the Aphorisms for the secret influence from the stars acting at a distance through interposing matter, and his copy of Peregrine's De Magnete survives, heavily underlined and annotated (1562) — but it is not possible to fix the exact period when he devised these instruments.
[Dee sagt 1570 in seinem Vorwort zu Billingsley's Euklid, er habe den PC 'kürzlich', d.h. 1556/7, erfunden.] 
On the title page and in the preface to General and Rare Memorials (1576) he speaks of them as invented by him 20 years past, but he was possibly predating these inventions to rebut more thoroughly a counter claim to the invention of the paradoxall compass, advanced by [?]James Alday perhaps, Professor Taylor suggests — some little while previously and which Dee, aggrieved, notes among the other manifold injuries done him by his countrymen. Of the exact nature of the paradoxall compass we have no knowledge, for Dee though he promised to append a full description of it to General and Rare Memorials failed to do so. It seems likely however that it was designed to overcome certain difficulties connected with sailing in the polar regions where the considerable dip of the needle and the convergence of the meridians resulting in a close spiralling of the t[r]humbs, made accurage navigation almost impossible. Professor Taylor suggests that "This Paradoxall Compass enable the master to lay a course along a successio of rhumbs which would make an approximation to great circle sailing," and that it was a practical development of certain teachings of Pedro Nunez. It is possible that it embodied an adjustable rose to be used in conjunctions with the compass of variation. From some papers of Dee's bearing on his invention, it might appear that it was as much a new method of computing data, by the aid of sets of  tables, as a mechanical instrument, and was perhaps intended as a way of achieving the same advantages, while employing the standard charts of the time, as Mercator's charts on which loxodromes could be drawn as straight lines, later offered, though only for fairly low latitudes. Whatever its details, it apparently came into fairly general use as John Davis' list of instruments essential to a "Skilful Seaman" in 1595 runs "Sea Compasse, a crossestaffe, a Quadrant, an Astrolabe, a Chart, an instrument magneticall for the finding of the variation of the compasse, an Horizontall plane Sphere [!], a Globe and a paradoxall compasse." "By which instruments all conclusions and infallible demonstration, hidrographicall, geographicall, and Cosmographicall, are without controlment of errour to be performed." 
[Vergleiche weiter unten. Die folgende Bemerkung der Thesis hinsichtlich des Dee'schen Variationskompaß geht insofern fehl, als das Zitat den Paradoxen Kompaß bezielt, nicht den Compass of Variation:]
Dee's compass and his view of variation probably lies at the base of his assertion in 1576 [General and Rare Memorials] that he had devised a method for the determination of longitude even "without sight of sonne moone or star".
[Mittels des Paradoxen Kompaß ist eine derartige Bestimmung allerdings möglich. Wenn ich richtig sehe, handelte es bei Dee's Variationskompaß um die Nacherfindung des Sonnenkompaß von Pedro Nunes, der 1542 vorschlug, 
mit einer Kombination von Kompaß und Sonnenuhr die magnetische Deklination am Ort der Messung festzustellen. Peter Apian beschrieb derartige Messungen schon 1524 in seinem Cosmographus Liber (col.51), wiederum 1529 in seiner Cosmographiae introductio. Er benutzte eine Kombination aus Kompaß und Sonnenuhr dann 1533 in seinem Instrument Buch und lieferte 1540 schließlich eine ausführliche Beschreibung und Handreichung zur Messung lokaler Mißweisungen per organum viatorum (quod vulgo Compassus dicitur), Cosmographia 1540, f.XXIVv, hg. von Gemma Frisius bei Birckmann-Coppens.]
be plotted
Erstaunlich ist, daß Frau Taylor - und mit ihr ihre "englische" Schule - die sprachlichen Feinheiten John Dee's nicht zur Kenntnis genommen hat: Bei der ersten Erwähnung des "Paradoxen Kompaß" schreibt Dee von ihm in der Mehrzahl, was gewiß nicht ohne weiteres auf mehrere Instrumente der gleichen Art schließen läßt. Siehe den originalen Text später.

to solve the problem
Meine Überlegungen führen - im folgenden - zu einem anderen Ergebnis: 
  • (1) "The paradoxall compass" ist nichts anderes als die Dee'sche Bezeichnung der "paradoxen Rhumben", der schiefläufigen Rhumben des Pedro Nunes 1533ff und des Gerhard Mercator 1541 / 1548ff. "The paradoxall compas" interpretiert das seltsame Verhältnis zwischen den Richtungen, die ein Kompaß anzeigt, und deren "paradoxe" - nicht-geradlinige - Darstellung auf dem Globus bzw. in allen Karten - außer der einen, die zum Zeitpunkt der Dee'schen "Entdeckung" allerdings noch nicht auf dem Markt war: Gerhard Mercators Karte ad usum navigantium. Der Kompaß ist einfach "paradox" - er spielt "verrückt" - , weil er nicht einen geradläufigen, sondern einen schiefläufigen (spiraligen: loxodromen) Kurs anzeigt.
  • (2) Mit seinen Tafeln löst John Dee daher das Problem des kompaßorientierten Segelns (seines Zeitalters) unabhängig von irgendeiner Kartenform - sei es in Verbindung mit einer Marinus-Plattkarte (plain chart), sei es in Verbindung mit der ersten Ptolemäus-Projektion oder auch der zweiten = Stab-Werner-/Bonne-Projektion, von späteren Kartenformen ganz zu schweigen.


Wie 1541 von Gerhard Mercator schon - aber rein konstruktiv - geleistet, gibt Dee den Seeleuten ein Mittel an die Hand, die "klassischen" Rhumben auf jedweden Erdglobus / auf jewede Seekarte  aufzubringen. Und nicht nur das: offenbar hat er die Piloten mit Hilfe seines canons angeleitet, das Großkreissegeln mit Hilfe des Rhumbensegelns zu approximieren.

  • Nur eins gelingt ihm mit seinem Tafelwerk nicht: die ingeniösen Vorstellungen von der Lösung der Probleme der zeitgenössischen - und nicht nur dieser - Seefahrt mittels einer geraden diesen Problemen angemessenen Karte, eben ad usum navigantium, aufzulösen. Das ist seinem kontinentalen Freund, the very principal Authority whereupon, Gerhard Mercator, vorbehalten geblieben. Daß auch die "klassischen" Aufgaben eines Piloten mit Hilfe eines geeigneten Ansatzes (s.w.u.) werden können, das werde nicht bestritten.
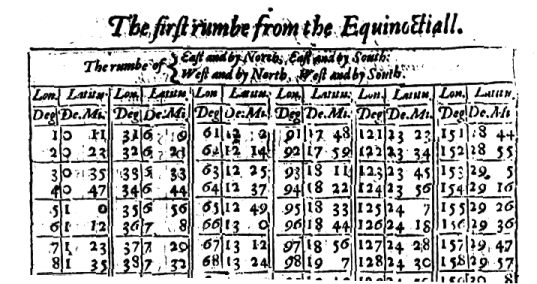
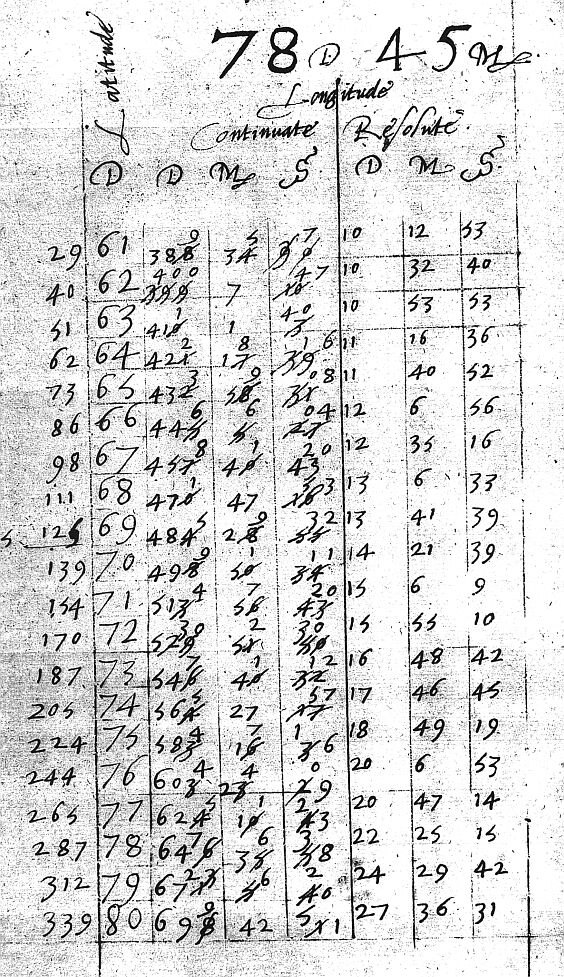
describe
Damit wird jetzt wohl hinreichend klar, daß es sich beim "Paradoxen Kompaß" nicht um ein Instrument, sondern vielmehr um eine einzelne bzw. um das System aller Strich-Rhumbe(n)-Tafel handelt.
Paradoxie
Im Jahre 1595 wurde das Segeln mit Hilfe der Richtungstafeln des John Dee erstmalig von John Davis in seinen Seamen's Secrets dargestellt. Vgl. E.G.R.Taylor: Bourne S.416. Noch kann ich mir nicht vorstellen, wie Davis dies ohne die Tafeln Dee's geleistet haben kann. (Die Seamens's Secrets habe ich noch nicht einsehen können. Das Davis-Zitat weiter oben zeigt eigentlich nur an, daß Davis eine Ahnung vom Dee'schen Euklid-Vorwort gehabt haben muß.) 

Verbesserung
Vergleichen wir allein die Genauigkeit der Beziehungen zwischen den Breiten- und den zugehörigen Längendifferenzen, so ist der Fortschritt z.B. von Enciso und sogar von Nunes zu Dee immens: 
    Rekonstruieren wir aus den Strichtafeln beider die Strichwinkel - z.B.- für den siebten Rhumb, so erhalten wir anstelle von 78.75° bei 
    • Enciso    77.28°
    • Nunes     78.67°
Bei Dee dürfen wir getrost von präzise 78.75° ausgehen. 
    Die Segelstrecke von 87.1/6 Leguen im siebten Rhumb hat bei 
    • Enciso eine Längendifferenz von rd. 4° 51' bei portugiesischem Maß bzw. von rd. 5° 6'  bei spanischem Maß zur Folge.
    Die entsprechende Segelstrecke von 89.3/4 Leguen im siebten Rhumb hat bei
    • Nunes eine Längendifferenz von rd. 5° 2' - bei portugiesischem Maß - zur Folge.
John Dee hat 5° 1' 39''.
Berater
Das Vor-Wort John Dee's zum Brief Gerhard Mercators vom 20. April 1577 - vergl. E.G.R.Taylor, IMAGO MUNDI XIII, 56ff - zeigt in aller Deutlichkeit, daß John Dee höchst interessiert nach den nördlichen Passagen Ausschau hielt: 
"And this matter of Discovery in hand, and chiefly of these most Northerly Countries and Iles, hath caused me (since last yere) to send into divers places beyond the sea, and to men there in our age rightfully [esteemed, to wit to the] honest Philosopher and Mathematician, Gerardus Mercator, ... In as much as, speedily he returned the very principal Authority whereupon he fasshioned unto us that strange plat [d.i. die Karte des Nordens im südwestlichen Teil der Weltkarte 1569] of the Septentrionall Ilands. That thereby our men (Adventures and Discoverers) might understand, what account is to be made, or what Credit is to be given to the same Description."


Der Brief Gerhard Mercators an John Dee enthielt einen Auszug aus dem Reisebericht des Jakob von Knoyen aus 's-Hertogenbosch - wir kennen ihn schon von der Weltkarte 1569 her - , den er zusammen mit anderen Berichten - u.a. der Gestae Arturi, der Inventio Fortunatae - der Konstruktion der nördlichen Länder in der Weltkarte 1569 zugrunde gelegt hatte. Die Karte des Nordens - Dee: the strange plat - hatte Gerhard Mercator seinem Schreiben offenbar beigefügt.


wahren Seekarten
Vgl. z.B. oben: Charts Hydrographicall, true, (not with parallel Meridians). - darin war und blieb er ein treuer Schüler des Claudius Ptolemäus, dem schon der Zylinderentwurf des Marinus von Tyros nichtswürdig erschien: Beiden fehlten auf quadratischen Plattkarten die Repräsentation der gekrümmten Kugeloberfläche.

Andeutungen
Pedro Nunes, Mathematiker in Coimbra und Kosmograph des portugiesischen Königs, hat die portugiesischen Hydrographen und die westwärts fahrenden Kapitäne mehrfach darauf hingewiesen, daß die Kursgleichen des kompaßorientierten Segelns auf hoher See, die alle Meridiane unter konstanten Winkeln schneiden, sowohl auf dem Globus als auch in der quadratischen Plattkarte gekrümmte Linien seien, also keineswegs mit den geradlinigen Rhumbenlinien der Kompaßrosen der Seekarten übereinstimmen. 

Schon 1533, als er sich zum ersten Mal in einem "kleinen" Tratado über die ihm von Martim afonso de Sousa vorgetragenen Bedenken über gewisse Praktiken in der Kunst des Segels geäußert hatte (pequeno tratado: sobre certas duuidas: que trouxe Martim afonso de Sousa .... nam somente cousas praticas da arte de nauegar),  haben weder die Globenmacher noch die Hydrographen noch die Piloten ihn in seiner Kritik verstanden: ihre Skrupel, aber auch ihre Verwechslung der "vulgären Regeln" der Segelkunst mit den Begriffen und Anweisungen der Wissenschaft (escrupoloso em misturar com regras vulgares desta arte / termos & pontos de sciencia) konnte er nicht beheben, owohl er ihnen schon damals in aller Deutlichkeit den Unterschied zwischen dem einfachen - "falschen" - Segeln auf einem Windstrich und dem kompaßgerechten - "wahren" - Segeln verdeutlicht hatte:
Die Linie .d.c.e. ist die "gewöhnliche" Rhumbe NW. Aber das Segeln nach diesem Windstrich folgt im Wahrheit nicht dieser geraden Linie, sondern der Kurve .a.c.b., die in Wirklichkeit weder einem Kreis noch einer geraden Linie gleicht. Und das ist seiner Vorstellung nach die Auffassung,  aus der der Fehler der Piloten (nauegantes) entspringt. Sie folgen einer falschen Information (falsa enformação), sollten aber eigentlich der Wahrheit folgen.

 
  • Es handelt sich bei der vorstehenden Zeichnung um die ?erste Darstellung (1533) des Unterschieds von Windstrichen in der Plattkarte und den ihnen entsprechenden kompaßorienten "paradoxen" Rhumben. 
Die Piloten folgen den Windstrichen der Plattkarte (erste Methode), besser aber sollten sie auf Abschnitten von Großkreisen segeln (zweite Methode) - wenngleich sie in beiden Fällen die Kurse dauernd zu ändern haben..
In seiner nautische Schrift "Tratado fez em defensam da carta da marear", der portugiesischen Übersetzung der Sacrobosco-Sphäre "Tratado da sphera" 1537 beigebunden, kommt Nunes auf seinen "kleinen Tratado" von 1533 zurück und verteidigt vehement die Benutzung der "gemeinen" Plattkarte, deren nautische Mängel William Bourne noch 1574 rügt und vor deren "naiver" Anwendung er warnt, außer "if the platte be truely made". Aber "truely made" war keine von ihnen. 

Auch der Hinweis des Nunes, anstelle einer Generalkarte einzelne Zonenkarten mit korrekter Zuordnung des Äquators zu deren Mittelbreiten (vera similitudo vel ratio) zu verwenden, fand kein Echo. Und nahezu zornig tadelt er die Globenmacher Lissabons dafür, daß sie mehr Sinn für Ornamentik als für Genauigkeit hätten.

Sollte Gerhard Mercator die Schrift des Pedro Nunes bis 1539 kennengelernt haben - in diesem Jahr begann er spätestens mit der Konstruktion seiner Erdkugel von 1541 - , so scheint er der einzige gewesen zu sein, der Nunes verstanden hat.

Daß die Schrift des Nunes Löwen in zwei Jahren erreicht haben kann, ist bei dem regen Seehandel der Spanier und Portugiesen mit | über Antwerpen durchaus möglich. Dennoch würde dieser Sachverhalt nicht im geringsten die Großartigkeit des Loxodromenentwurfs von 1541 und erst die Konstruktion der Weltkarte von 1569 schmälern: Niemand sonst - bis eben auf John Dee in den Jahren 1557-1558 - hat in den Jahren von 1533 bis 1569 die Aufgabe des Nunes so gut verstanden und zweimal treffend - öffentlich -  umgesetzt, - letzteres hat selbst Nunes nicht geleistet.
Daß John Dee nach seinen Besuchen in Löwen mit Pedro Nunes in Verbindung getreten ist, macht zumindest der Widmungsbrief der Propaedeutmata Aphoristica vom 20 Juli 1558 plausibel: Da er fürchtete, unter der Verfolgung und Anklage durch seine religiösen Widersacher in London womöglich sein Leben zu verlieren, hat er neulich Pedro Nunes inbrünstig gebeten, illumque obnixe nuper oravi - jenen Mann, der die Künste der Mathematik auf das Höchste beherrscht - , seine noch unvollendeten Werke, die Nunes nach seinem Tode überbracht werden sollen, mit der gehörigen Sorgfalt herauszugeben. Dee ist von der Loyalität Nunes' überzeugt: cum & me tam amet fideliter, denn dieser liebe ihn auf treuherzige Art und Weise.
Es könnte durchaus sein, daß die beide Bücher De nova Navigantionum ratione, Lib.2, die gesamte Materie des hier in Rede stehenden "Segelns mit Hilfe des Paradoxen Kompaß" enthalten haben. Und es könnte durchaus sein, daß Dee aus einem Schriftwechsel mit Nunes die bei Gerhard Mercator (1547ff.) noch ausstehenden Hinweise über den approximierenden Zusammenhang von Großkreis- und Kursgleichen-Segelns erhalten hat.
Frage
Es scheint auf den ersten Blick ein wenig überraschend zu sein, daß John Dee den Zusammenhang zwischen der Breitenänderung Dj  und der zugehörigen Längenänderung Dl herstellt und nicht die Umkehrbabbildung    verwendet.
Die Strichtafeln  beschreiben bekanntlich die Abbildung   : Die "vulgäre" Technik des Breitensegelns favorisierte diese Abbildung/Zuordnung.


Edward Wright tabelliert 1599 die Funktion    :
 

Verständlich wird die Zuordnung    aber aus der Überzeugung Dee's, daß wahre Seekarten solche mit gekrümmten Längengraden sind. Die Breitengrade haben konstante Abstände von  = 1° voneinander, die Längengrade dagegen gegen Norden | gegen Süden veränderliche, - d.h. genauer: von  abhängige Abstände voneinder:   ().


Gleichung
Vgl. z.B. Duisburger Forschungen Bd. 41, S.62: Die Loxodromengleichung.
Indem wir die Hilfsgröße h aus den Gleichungen elimieren, erhalten wir den uns interessierenden Zusammenhang zwischen , ,und. 

zu bestimmen trachtete
Hätte John Dee nicht die Zuordnung Breitendifferenz Längendifferenz auf die "klassischen" Rhumben = Striche des Seemanns beschränkt, sondern - wie Gerhard Mercator und später Harriot, Wright, Snellius ... - die Zunahme der Breitendifferenzen in Abhängigkeit von der erreichten Breite in ihrer vera ratio zum Äquator berechnet: (), er wäre der Entdecker | Erfinder der Tafel der Meridionalteile geworden.

Dieses Argument zeigt erneut, daß John Dee sich einer speziellen, keiner generellen Lösung der loxodromischen Aufgabe des Jahrhunderts gestellt hat.


Entwicklung
Henri Bond hatte schon 1645 in einem Zusatz zu Richard Norwoods Epitome of Navigation angegeben, that the Meridian Line was Analogous to a Scale of Logarithmick Tangents of half the Complemente of the Latitudes, wie Edmund Halley in seiner Easy Demonstration of the Analogy of the Logarthmick Tangents to the Meridian Line or sum of secants, Philosophical Transactions 19, Nr.219, Jan./Feb.1696, 202, anmerkt.
Zur Geschichte vgl. man Jos.E.Hofmann:Nicolaus Mercator (Kauffman), Akademie der Wissenschaften und der Literatur, Math.-Naturwiss. Klasse 1950, Nr.3.

Korrekturen

Methode der Mittelbreiten
Diese wendet später (1599, 1610) auch  Edward Wright an, William Oughtred schlägt 1632 (London), 1660 (Oxford) in seinem Circle of Proportion and the horizontal Instrument noch feinere Unterteilungen vor.

Formel
Wie eine solche mit Hilfe differentialgeometrischer Überlegungen abzuleiten ist, habe ich in den DUF 41 S.62ff. gezeigt. Vergleiche die Anmerkung GLEICHUNG.

sec-Tafel
Die erste sec-Tafel des Jahrhunderts hatte Copernicus um 1530 aufgestellt; bekannt wurde sie erst in der Mitte des 19.Jhs. Die Funktion secans dagegen benutztEdward Wright in seinen Certaine Errors von 1599. Er setzt also einen Leser voraus, der auf der Höhe der Zeit ist und die Trigometrie beherrscht:
Bodleian: e-mail: bis auf weiteres ...
Return-Path: ×pab@bodley.ox.ac.ukØ
Received: from bodley01.bodley.ox.ac.uk ([163.1.108.21])
by clubserv.rp-online.de (8.9.1a/8.9.1) with ESMTP id PAA12675
for <Wilhelm.Krücken@mail.online-club.de>; Tue, 15 Jun 1999 15:28:25 +0200 (METDST)
From: Patricia Buckingham ×pab@bodley.ox.ac.ukØ
Subject: MS. Ashmole 242

Mr.Wilhelm Krücken,
Zeppenheimer Strasse 9,
40489 Düsseldorf,
Germany
 

Dear Mr. Krücken, 

Thanks for your e-mail of 2 June, and apologies for the delay in replying.

MS. Ashmole 242 is a large miscellany of several sections bound together, mostly on the subjects of astrology and astronomy. The sections are by several different writers, and were originally separate and unrelated. 

Fols. 139r-153v, the 'Canon Gubernauticus' in Dee's hand, is followed by two further short sections also in his hand, written in reverse: 'an arithmetical treatise on fractions'
(fols. 160v-156v); and 'Questions and observations about draining and imbanking the Fens' (fols. 156-154). 

Neither of these would appear to be what you seek, and the other materials in MS. Ashmole 242 do not appear to relate to Dee.

The Ashmole collection contains a vast quantity of further material by or about Dee, scattered across dozens of volumes. We have tried looking up 'trigonometrical figures' under his name in the index to the Ashmole catalogue, but without success.
 

I regret that we are unable to spend any more time in searching for this material, in the few minutes available for any single enquiry. However, if you are able to provide a more specific reference (Bodleian shelfmark and folio number) from your own reading in the secondary sources, we should of course be happy to consider another photographic order from you.


Yours sincerely,
 

Tricia Buckingham 
Senior Library Assistant