|
Rechnen wir!
Hätte Gerhard Mercator
-
a) gerechnet: den Beweis des Zusammenhangs beider Approximationen rechnend
aufgestellt, und
-
b) die Anfänge der Reihenrechnung von
den mathematicis seines Zeitalters übernommen,
so wäre ihm allein mit den Mitteln der Bruchrechnung eine qualitativ
ansprechende Einschachtelung für p gelungen.
Denn aus
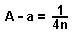folgt leichthin:
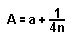Zusammen mit 8a < k < 8A folgt daraus
19. 
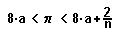
Aus den Sätzen 9,15 folgt schließlich
20. 
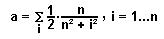
Wenn wir dann noch den Mittelwert aus beiden Grenzen errechnen, erhalten
wir z.B. für n=50,100 ganz respektable Schulstuben-Ergebnisse.
Es ist - natürlich - heutzutage nicht schwer, die Approximationen
z.B. mit einem "kleinen" PASCAL-Programm durchzuführen. Damals
hätte es schon eines beträchtlichen Rechenaufwandes bedurft,
um die folgenden Näherungen durch das arithmetische Mittel der jeweiligen
Grenzen zu finden:
n
=50 |
k
= 3.1415259869 |
D
= 0.0000666667 |
| =100 |
= 3.1415759869 |
= 0.0000166667 |
| =500 |
= 3.1415919869 |
= 0.0000006667 |
| =1000 |
= 3.1415924869 |
= 0.0000001667 |
| =5000 |
= 3.1415926469 |
= 0.0000000067 |
| =10000 |
= 3.1415926519 |
= 0.0000000017 |
Archimedes hatte u.a. die Kreiszahl durch 22/7 = 3.1428571
angenähert, Ptolemaios - in sexagesimaler Schreibung - durch
3°8'30"
= 3.1416667, Dürer "mechanice"
durch 25/8 = 3.125. Indem
Vieta (1540-1603)
1593
das archimedische Verfahren der Ausschöpfung durch regelmäßige
Polygone bis zum 393216-eck fortsetzte, gelang es ihm, p
durch das arithmetische Mittel 3.1415926536 bis auf 9 Stellen genau
darzustellen!
Reihenrechnung
Er besaß die Arithmetica integra,
Nürnberg1544,
des Michael Stifel (1487-1567)
und hätte aus ihr die Reihenrechnung lernen können!
Dürer
Der Wert Dürers findet sich in der Architectura
des Vitruv - Gerhard Mercator besaß ein Exemplar der
Architectura
(aus ihr hat er u.a. den zentrischen Umlauf von Merkur und Venus um die
Sonne entnommen) - und ist sort dem römischen Duodezimalsystem recht
gut angepaßt. |