Paradigmenwechsel

Um von den loxodromischen (den logarithmisch-bestimmten) Größen zu allein rationalen übergehen zu können, errichten wir in S die Tangente ST. Wir zerlegen ST in n kongruente 
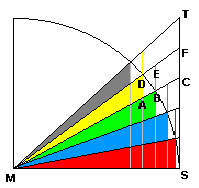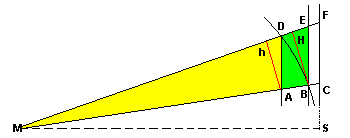Teilstrecken (z.B. CF = 1/n). Die Teilpunkte verbinden wir mit M. Durch die Schnittpunkte der Sekanten mit dem Kreis errichten wir die Senkrechten auf MS, d.s. Parallelen zur Tangente ST. 

Wir wählen das Dreieck MCF zur i.ten Teilfigur, an der wir weitere Überlegungen anstellen. Zusätzlich konstruieren wir die Höhen h und H der Dreiecke MAD und MBE: 

Nach den Strahlensätzen folgt: 

1. 
2. 

Wir bezeichnen die Flächen (bzw. die Maßzahlen) von MAD und MBE mit ai und Ai . 
Für diese Flächen gilt: 

3. 
4. 

Für ihr Verhältnis folgt dann 

5. 
6. 

Setzen wir nun nach den Sätzen 1, 2 entsprechend ein, erhalten wir: 

7. 
d.h. die Flächenmaßzahlen beider Dreiecke verhalten sich wie die Quadrate ihrer Grundseiten. 
Wenn wir den Quadranten um 90° drehen, erkennen wir sofort: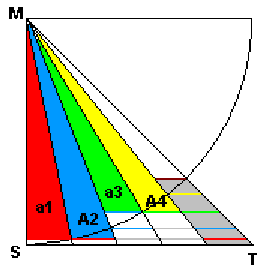 

8. 

denn die betreffenden Dreiecke haben die gleiche Grundseite und dieselbe Höhe. 

Summieren wir über i = 1...n, so gelte: 

9. 
10. 
Bilden wir die Differenz A - a , so fallen wegen Satz 8 alle Mittelglieder fort, und es gilt: 
11. 
Da die Trapeze zwischen benachbarten Parallelen gleichgroß sind (benachbarte Grund- bzw. Deckseiten sind gleichlang), folgt, daß die Differenz A - a unmittelbar zu schauen ist: A - a ist gleich der Flächenmaßzahl des grau eingefärbten Trapezes im letzten Sektor. 
Wir "sehen", daß mit größer werdendem n das Differenztrapez beliebig klein / schmal gemacht werden kann: So wie die "vergrößerten Breitenabschnitte" der Karte von 1569 - in der Zeichengenauigkeit - beliebig genau ausfallen, wenn nur die Breitendifferenz hinreichend klein gemacht wird, so nähern wir uns dem achten Teil der Kreiszahl k=pumso besser, je größer wir n wählen. 

Nun gibt sich die Mathematik mit derartig qualitativen Aussagen nicht zufrieden, sie verlangt einsichtig arithmetisch formulierte Aussagen, um die 100 Jahre nach Gerhard Mercators "Entdeckungen" üblich werdenden "Grenzwertbetrachtungen", Betrachtungen der später so genannten "infinitesimalen" Art, anstellen zu können. 


Größen
Hätte Gerhard Mercator die Sehnenrechnung des Ptolemäus auf die Kreissektoren MBD angewandt: den Bogen BD also durch die Strecke BD ersetzt und gerechnet, so hätte er den Gedankengang des Archimedes aufgenommen, dabei aber die Funktion sinus anwenden müssen; hätte er die "loxodromischen" Dreiecke BED zur Fehlerabschätzung herangezogen, so hätte er die Funktion secans kennen müssen. Weder das eine noch das andere können wir - bis auf den Tag - den arithmetisch-"spekulativen" Kenntnissen Gerhard Mercators zurechnen: Seine Einsicht in das Problem der Kreisquadratur war offenbar allein intuitiver Art. 

Teilstrecken
Wir vereinfachen ab jetzt unsere Sprechweise und identifizieren die geometrischen Objekte mit ihren Attributen: Wir sprechen z.B. von dem Objekt Radius r = MS und bezeichnen gleichwohl auch seine Länge |r| = |MS| mit "r" ( r = 1 ). 

Teilpunkte
Gerhard Mercator ist bei der Konstruktion der "vergrößerten Breitenabschnitte" von einer kongruenten Teilung des Quadranten (d.h. des rechten Winkels bei M) ausgegangen. Der Übergang von dieser kongruenten Winkelteilung zur kongruenten Streckenteilung der Tangente ST macht die ("rationale") Arithmetisierung seiner Konstruktionsfigur möglich. 

bezeichnen
Im weiteren unterscheiden wir auch nicht die Anführung und den Gebrauch von Buchstaben.