|
der loxodromischen Abbildung ist hinreichend bekannt:
Kann ein Kreis einem Quadrat der Flächenzahl nach gleich sein, oder - geometrisch formuliert - kann ein Kreis allein mit Zirkel und Lineal in ein flächengleiches Quadrat verwandelt werden? Von Anaxagoras (?500-?425) war seinerzeit überliefert, daß er "im Gefängnis die Quadratur des Kreises aufgeschrieben" habe, und Ammonios (?445-?526) berichtet, daß "die den Kreis Quadrierenden nicht danach forschten, ob es möglich sei, daß ein dem Kreis flächengleiches Quadrat existiere, sondern in der Meinung, daß es so sein könne, versuchten sie, ein dem Kreis flächengleiches Quadrat zu erzeugen". Entstanden war das Problem offenbar in der pythagoreischen Schule des sechsten bis fünften Jahrhunderts v.Chr., da man entdeckt hatte, daß die Seite eines dem Kreis einbeschriebenen Quadrats inkommensurabel zum Radius des Kreises ist. Nun vermitteln die konstruktiven Elemente der Methode von 1569 zwar einen intuitiven Zugang zur Annäherung der Kreisflächenzahl p, aber keinen geometrisch-konstruktiven, sondern allein auf dem Wege über das Problem der "Ausschöpfung" des Kreises durch Polygone einen arithmetischen. "Intuitiv" muß für Gerhard Mercator "wahr" gewesen sein, daß durch die fortwährende Verbesserung der Annäherung des Achtel-Quadranten durch die einbeschriebenen wie umbeschriebenen Polygonflächenzahlfolgen die Kreiszahl k - die Ludolf van Ceulen später PI ( p ) nennen sollte - zwischen einer "inneren" Flächenzahl a und einer "äußeren" A "beliebig genau" eingeschachtelt werden könnte: 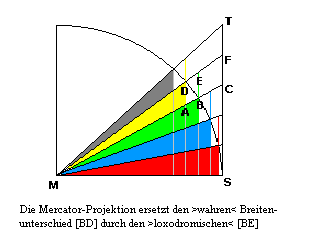 "Berechnet werden kann", dazu sehen wir ?nirgends einen Ansatz bei Gerhard Mercator, aber wir wollen zeigen, daß auch hier seine Intuitionen mit den Mittel seiner mathematischen Kenntnisse nachvollzogen, rekonstruiert und damit erklärt und erhärtet werden können. Wir benötigen nicht mehr und nicht weniger, als seine Idee von der Gleichartigkeit beider Probleme aus dem Geometrisch-Konstruktiven des ersten in das Arithmetisch-Rechnende des zweiten umzusetzen. Man vergleiche die Duisburger Forschungen Bd 41, S.1/2. Oder auch PM 4/36 S.145ff, Jg.1994. Problem In Albrecht Dürers Underweysung der messung mit dem circkel und richtscheyt, 1525, heißt es: "Vonnöten wäre zu wissen Quadratura circuli, das ist die Gleichheit eines Zirkels und eines Quadrates, also daß eines ebenso viel Inhalt hätte als das andere. Aber solches ist noch nicht von den Gelehrten demonstrirt. Mechanice, das ist beiläufig, also daß es im Werk nicht oder nur ein kleines fehlt, mag diese Gleichheit also gemacht werden. Reiß eine Vierung und teile den Ortsstrich [die Diagonale] in zehn Teile und reiße danach einen Zirkelstrich, dessen Durchmesser acht Teile haben soll, wie die Quadratur deren 10." (!Wurzelrechnung führt dann auf p = 25/8.) Ammonios Man vergleiche die Eudoxus-Studien von Oskar Becker. Es ist Anaxagoras, der den Begriff des Unendlichen von Anaximander aufnimmt, als Erster in der Geschichte des Unendlichkeitsproblems ihm aber diejenige rationale Form aufprägt, die ihn für die Mathematik brauchbar werden läßt - nämlich in der Form eines infinitesimalen Prinzips: "Im Kleinen gibt es kein Kleinstes, sondern es gibt immer noch ein Kleineres. Denn was ist, kann durch keine noch so weit getriebene Teilung je aufhören zu sein. Aber auch im Großen gibt [es kein Größtes, es gibt] immer noch etwas, was größer ist." (Diels: Fragmente der Vorsokratiker, 46 A 38, Fragment 3). Alleine schon die Erzählungsform setzt voraus, daß "alle Welt wußte", daß Anaxagoras das Problem nicht nur behandelt, sondern auch gelöst hat: diese Ausschmückung schadete der Authentizität keinesfalls inkommensurabel D.h. beide Größen sind keine geeigneten bruchzahligen Vielfachen von einander: sie stehen in einem irrationalzahligen Verhältnis zueinander. Ausschöpfung Die Konstruktion der Karte AD USUM NAVIGANTIUM verblieb ganz im Geometrisch-Konstruktiven; Rechnungen waren nicht erforderlich, da die "vergrößerten Breitenabschnitte" in einer geeigneten Zeichung mit dem Zirkel abgegriffen werden konnten. Ein Übergang zur Arithmetik, zum Rechnen, findet aber stets statt, wenn Maßzahlen von geometrischen Größen zu bestimmen sind. So lassen sich zwei Strecken ihrer Größe - d.i. ihrer Länge - nach durchaus konstruktiv mittels Streckenabtragung oder Parallelverschiebung vergleichen, sogar die Relation "hat dieselbe Länge wie" - prädikativisch formuliert: "haben dieselbe Länge" - läßt sich durch Abstraktion nach der geometrischen Relation der Kongruenz definieren:
Unser Problem handelt also von der Berechnung der Kreiszahl p . |