 |
 |
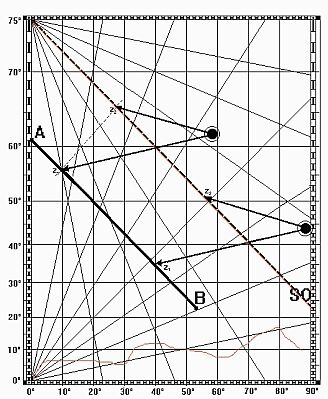
Gegeben seien die beiden Orte A und B; gesucht
ist der Kurswinkel k gegen Nord.
Den ersten Ort, sagen wir A, tragen wir auf dem 0.ten Längengrad seiner Breite jA nach ab. Nachdem wir den zweiten Ort entsprechend den vorgegebenen Längen- und Breitendifferenzen in die Kurstafel eingetragen haben, richten wir den oberen - in (0° | 75°) - oder - je nach Lage von B - den unteren Bindfaden - in (0° | 0°) befestigt - so aus, daß wir mit geeigneter Zirkelöffnung seine Parallelität zum Kurs AB feststellen können.5.2 2. Aufgabe: Bestimmung der loxodromischen Entfernung AB Gegeben seien die beiden Orte A und B; gesucht
ist ihre Distanz in Seemeilen.
Der Seemann nennt das in die Mercator-Karte eingetragene Besteck ABF das "vergrößerte Kursdreieck" oder kurz das "Mercator-Dreieck". Wenn auch - wie auf der ganzen Weltkarte - die Richtungen (die "directiones" Gerhard Mercators) als gerade Linien eingetragen werden können, so hat dies - wie wir gesehen haben - von Breite zu Breite eine Änderung des Maßstabes zur Folge.
|
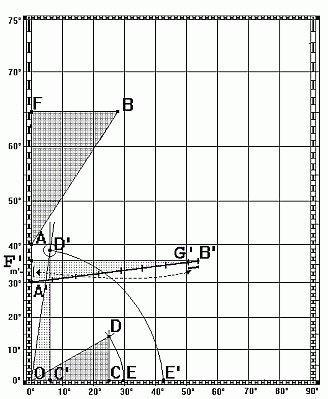 |
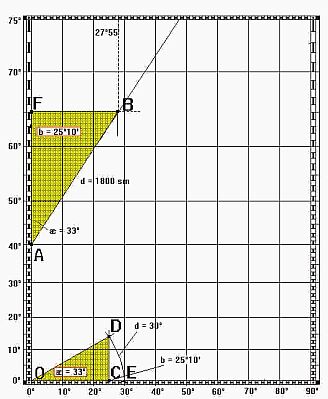
Wir tragen die beiden Orte wieder in die Kurstafel ein. Wir kennen oder messen den Kurs gegen Norden: k. Den Breitenunterschied tragen wir auf dem Äquator von O aus ab: C. An OC tragen wir den Kurswinkel k in O an. Wir errichten in C die Senkrechte, die den freien Schenkel des Kurswinkels in D trifft. Die Strecke OD tragen wir von O aus auf dem Äquator ab: E. Die in OE enthaltenen Minuten sind die loxodromische Entfernung von A nach B (in Seemeilen gemessen: l' = l sm = 1852 m).
vorkommt, sind beide Dreiecke ähnlich. Nach dem 4. Lehrsatz des Euklid (B VI) folgt wieder:
AB : OD = AF : OC Þ AB = AF ·.(OD / OD).
Der Seemann nennt das am Äquator konstruierte Kursdreieck OCD auch das "wahre Kursdreieck". Es ist aber auch überzeugend, den Praktiker Gerhard Mercator
am Werke zu sehen.
Wenn nämlich ein Kurs nahe bei OST oder nahe bei WEST anliegt, dann ist der Schnitt der beiden Geraden OD' und C'D' nurmehr "schleifend", so daß die Lage von E' unbestimmt wird.5.3 3. Aufgabe: Positionsbestimmung Gegeben seien der Ort A, der Kurs k und die zurückgelegte Strecke s [sm]; gesucht sind die Koordinaten (Länge | Breite) des Zielortes B. |
 |
Wir zeichnen A auf der Null-Länge unter der gehörigen Breite ein und legen den Kurs an. Irgendwo auf dem freien Kursschenkel muß B liegen.
AF : OC = AB : OD Þ AF = AB · (OC / OD).Da AB und OD = OE das gleiche Maß haben, stimmen AF und OC wieder in ihren Maßen überein.
Die Nautik lehrt exakt die Verfahren, die Gerhard Mercator an seiner Karten von 1569 als erster ersonnen hat.
Die Erweiterung der Projektionart Mercators auf die abgeplattete Erde führt C.F.Gauß durch. 1951 macht die NATO die UTM
- die Universale Transversale Mercatorprojektion - zur alle NATO-Partner
verbindende Kartenprojektion. (Die UTM unterscheidet sich von der
bei so genannten "Gauß-Krüger-Projektion" - die 1926
in Deutschland als Grundlage der staatlichen Landesaufnahme festgelegt
wurde - genau so wie eine quadratische von einer rechteckigen
Plattkarte: der Gauß-Krüger-Zylinder berührt
den jeweiligen Großkreis
Seit wir uns in der Geodäsie der Satellitenmessungen bedienen, liefert die UTM - in leichter Abwandlung entsprechend den Vorschlägen nach Krüger (1912) - das verbindliche Kartenmaterial. |