Spezielle Entwürfe
4.1 Die Mathematik der angeführten Abbildungen erweist sich i.A. als schwierig: 
  • ohne die Kenntnis trigonometrischer Funktionen scheint überhaupt nichts zu gehen.
Betrachten wir nur im Überblick einige Abbildungsbeziehungen.
azimutal-perspektive Entwürfe:
Alle azimutalen Kartenprojektionen mit einem Pol als Kartenmittelpunkt, haben Abbildungsbeziehungen der folgenden Art:
 
x  =  f(j) • cos(l)
y  =  f(j) • sin(l)
azimutal-perspektive
  Entwürfe mit
orthographisch  f(j) = R.· cos(j)
stereographisch  f(j) = 2 R · ctg(p/4 - (j/2)
gnomonisch f(j) = R · ctg(j)
azimutal-nicht-perspektive
  Entwürfe mit
mittelabstandstreu f(j) = R · (p/2 - j)
flächentreu f(j) = 2R · sin(p/4 - j/2)
Lambert-Entwurf:
:
Die Zylinderabbildungen von Lambert und Mercator haben wiederum eine gemeinsame Struktur:
 
Lambert Mercator
x = R · l. x = R · l
y = R · sin(j)  y = R · ln(tan(p/4 + j/2))
.
 
Mercator-Entwurf:
Die Mercator-Abbildung ist dadurch von den anderen Abbildungsarten unterschieden, daß in den allgemeinen Bedingungen [x=R·l und y=R·f(j)] die Funktion f so bestimmt wird, daß der Entwurf winkeltreu wird:
  • Die rechteckige (plane) Masche mit den Seiten dx und dy hat dabei 

    • (a) der Kugelmasche  mit den Seiten R·cos(j)·dl und R·dj zu entsprechen (Ähnlichkeit im Kleinen, daher die Differentiale), so daß 
    (b) die Diagonale der Kugelmasche ('Loxodrome' genannt) in die betreffende gerade Diagonale der planen Masche übergeht. Das aber heißt:
  • Die Steigung der planen Diagonalen dx/dy muß gleich der Steigung der Loxodromen werden, d.h. = dj / cos(j)·dl.

    • Mit dy = R·df(j) und dx = R·dl folgt daraus die Differentialgleichung für f:
df(j) = dj / cos(j)
Ihre Integration liefert - die Integrationskonstante C sei so gewählt, daß j = 0 Þ y = R·f(j) = 0 -
f(j) = ln [ tan (p/4 + j/2 ) ]
    so daß die Abbildungsgleichungen des Mercator-Entwurfs lauten:
    .
    • x = R · l
    • y = R · ln [ tan (p/4 + j/2 ) ]

      • .
      Wird die Forderung nach einem Entwurf mit zwei abweitungstreuen Breitenkreisen gestellt - +j0 und -j0 seien die betreffenden Breiten - , so folgt:
    • x = R · cos(j0) · l
    • y = R · cos(j0) ·  ln [ tan (p/4 + j/2 ) ]

.

  • Ohne hinreichende Elementarisierung - auch in heutigen Mathematik-Leistungskursen - scheint nach dem Vorstehenden eine schulunterrichtliche Lehre nahezu unmöglich zu sein - gäbe es nicht den exemplarisch-elementaren Zugang zur Projektion Gerhard Mercators über die Geschichte der Welt- und Seekarte von 1569.


Damit sind beim bei unserem eigentlichen Thema:
 

  • die historische Didaktik der Seekarte als methodischer Entwurf einer elementar zugänglichen Abbildung der Kugel auf die Ebene.
4. 2 Wie kam es zur Seekarte von 1569?
.
Das Ungenügen der Platt- oder Marinus-Karte stellte sich in dem Augenblick heraus, da die Portolankarten des Mittelmeeres, der englischen und atlantischen Küsten nicht mehr zureichten, da man sich zu Entdeckungsreisen auf die hohe See hinaus begab.

Ganz deutlich formulierte Martim Afonso de Sousa 1533 die Probleme der quadratischen Plattkarten, als er von einer Südamerikafahrt (1530-1532) nach Lissabon zurückkehrte:
 

  • Obgleich er - Kompaß-geleitet - den geraden Kurs (der Plattkarte) beständig eingehalten habe, habe er auf der Hinfahrt den Rio de la Plata um hunderte von Leguen (port. Meilen) nach Norden verfehlt. 
  • Und Pedro Nunes berichtet von einem Gespräch mit Martim, in welchem dieser seine Verwunderung darüber ausgedrückt habe, daß er auf der Heimfahrt - auf einem Großkreis unter einem bestimmten Anfangskurs segelnd - den Äquator nicht dort überquert habe, wo es eigentlich hätte sein sollen. 
Der folgende Ausschnitt versucht das Plattkarten-Problem klarzustellen: 

Kopiert man maßstabgleiche Marinus- und Mercator-Karten über einander, sieht man sofort, warum Martim die Einfahrt zum Rio de la Plata verfehlen mußte: 
  • Die Rhumben der Plattkarte täuschten ihm einen geraden Kurs vor, der in Wirklichkeit ein gekrümmter mit stetig sich änderndem Kurswinkel hätte sein müssen. 
  • Nur in der Mercator-Karte sind die Rhumbenlinien wegen des loxodromischen Längen- wie Winkelmaßes der Karte gerade Linien.
Zweimal trug Pedro Nunes - königlicher Kosmograph und Universitätsmathematiker zu Coimbra - den Kapitänen und Kosmographen in Lissabon die betreffenden Theorien vor, 
  • er unterschied zwischen orthodromen und loxodromen Kursen - wie wir heute mit Snellius sagen - ,
  • er zeigte den Unterschied des Segels auf Großkreisen und nach Kompaßstrichen auf,
aber keiner seiner Zuhörer hat ihn verstanden, - weder 1533 in direkter Reaktion auf die Fragen des Martim Afonso de Sousa, noch 1537, da er seine Überlegungen von 1533 zu einer Verteidigung des Gebrauchs der Plattkarte ausgearbeitet hatte:
 
  • Die Seekarten blieben vom Marinustyp. 
Im Gegenteil: diejenigen, die ihn - später schließlich - verstanden hatten, praktizierende pilotierende Seeleute kritisierten Nunes doch sehr heftig: die - allerdings mathematisch fundierten - Vorschläge des Nunes wurde offenbar nie praktiziert. 

Stellen wir uns also die nächsten Fragen:
 

Was sind Marinus-Karten?
Wie sind sie entstanden?
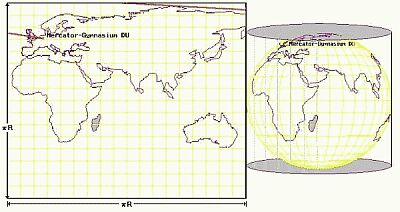Entstanden sind sie "ganz einfach" so: Marinus "wickelte" die Oikumene auf einen die Weltkugel im Äquator berührenden Zylinder längentreu ab. Und er konstruierte damit die erste "abstandstreue quadratische Plattkarte mit längentreuem Äquator".
Der schon im Klima von Rhodos - der Mittelmeer-Zone - auftretenden Verzerrungen wegen, soll er - nach Ptolemäus - sogleich eine zweite Karte konstruiert haben:
Was dem Äquator billig ist, das ist dem Breitenkreis von Rhodos teuer:
Das rekonstruierte Marinus-Original

Klicken Sie das Bild an (64 kB).
Marinus ließ den abbildenden Zylinder durch die Breite von Rhodos gehen, milderte damit die dort aufgetretenen Verzerrungen ab und erhielt eine rechteckige Plattkarte mit einem Längen- / Breitenverhältnis von 5:4, denn der Cosinus von 36° ist ungefähr 0.8 (= cos(36°)).

Daß die quadratische Plattkarte - rechteckige sind im 16.Jahrhundert äußerst selten - zur Seekarte wurde, konnte Marinus natürlich nicht ahnen, zumal Ptolemäus an ihr heftige Kritik geübt hatte: 

  • Von der - angeschauten - Krümmung der Erde blieb bei Marinus nicht viel übrig. 
Ptolemäus schlug daher zur Konstruktion von "angemessenen" Karten der Oikumene Kegelkarten vor, Karten seiner "ersten" bzw. "zweiten" Projektionsart, welch letztere schließlich im 15. und 16. Jahrhundert zur bevorzugten Projektionsart der Generalkarten = Weltkarten wurde.
Als Kegelabbildung stellt sie einen Sonderfall dar und gehört - mathematisch betrachtet - in eine Reihe mit den Entwürfen von Stab-Werner/Bonne, Finaeus/Mercator und Sanson/Flamsteed. - Das aber soll uns hier nicht weiter interessieren.

Die Mängel der Plattkarte führten Gerhard Mercator schon in den Jahren nach der Konstruktion seines Erdglobus (1541) zu intensiven Nachfragen. 1546 brachte er die Fehler der Karte in Zusammenhang mit der Nichtbeachtung der ja schon seit langem bekannten magnetischen Mißweisung des Kompaß. 
 
Aber so richtig fand er sich mit dem doch mehr systematischen Fehler der Projektionsart des Marinus nicht zu recht. Eine Abbildung der Erde zu finden, die seine '41er Loxodromen - von ihm directiones = Richtungen genannt - in Geraden der Ebene überführt, stellte sich trotz Nunes und Mercator-Globus als recht schwierig heraus.
Da er sich schon bei den Löwener Vorbereitungen für eine - epochen-machende - Europakarte intensiv mit der Geographie des Ptolemäus beschäftigt und inzwischen auch alle möglichen Entdecker-Berichte mit den dazugehörigen Seefahrtenhandbücher in Abschriften zur Kenntnis genommen hatte, leuchtete ihm allmählich das Prinzip einer "seefahrtstauglichen"
Plattkarte ein:
 
Marinus hatte rigoros alle Breitenkreise und damit alle Längenkreisabschritte auf die Dimensionen des Äquators gebracht, aber - im Grunde - "vergessen", die Breitenabstände diesen Verhältnissen anzupassen.
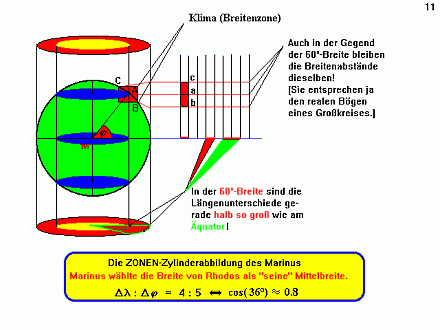Die quadratische Marinuskarte besaß nur einen einzigen abweitungstreuen Breitenkreis, - den Äquator; die rechteckige Plattkarte hatte deren zwei: 36°N. 36°S.

Die alles entscheidende Frage lautete:
 

  • Wie konnte diesem Mißstand abgeholfen werden? 


Im Prinzip so:
Da Gerhard Mercator sich in gehörigen Vorbereitungen für ein Lehramt in Kosmographie - mindestens an der Lateinschule zu Duisburg - auch wieder mit den ersten Büchern des Euklid beschäftigte, fielen ihm - dank der Hinweise 
  • im Seehandbuch des Francisco d' Enciso von 1530, b.ix v. - b.x r.
  • im Vorwort der Ptolemäus-Ausgabe von Willibald Pirckheimer aus dem Jahre 1524
und gewiß auch 
  • beim wiederholten Lesen der Untersuchungen des Pedro Nunes von 1537 
Anfang der 60er die Schuppen von den Augen:
 
1. Wie wäre es, wenn man die Konstruktion des Marinus, die ja schon zu einem Breiten-Längen-Verhältnis von 5:4 , also zu einer relativen Vergrößerung der Breitenabstände bei einer entsprechenden Verkleinerung der Äquatordistanzen - wenn auch zu einer überall gleichgroßen - geführt hatte, Breite für Breite wiederholen würde? 
2. Wenn man - statt die Breitenabstände beizubehalten und die Längenabstände betreffend zu verkleinern - genau umgekehrt vorgehen würde: Wenn man die Längendistanzen in der Größe der Äquatordistanzen beibehielte, dafür aber die Breitenabstände proportional vergrößerte?
Wie würde das für die Rhodos-Karte aussehen?
 
  • Bei einer Breitendistanz von l haben wir die Rhodos-Distanz auf 80% der Äquatordistanz verkleinert.
  • Wir müssen also 0.8 = 4/5 mit 5/4 multiplizieren, um die Rhodos-Distanz auf Äquatordistanz zu vergrößern.
  • Wenn wir aber die verkleinerte Distanz auf  l vergrößern, dann müssen wir den Breitenabstand l proportional, "entsprechend" vergrößern.
  • Indem wir l mit dem "Vergrößerungsfaktor 5/4 multiplizieren, erhalten wir einen neuen, vergrößerten Breitenabstand: 
  • der neue beträgt für die Rhodosbreite 125% der Marinusbreite von l.
In der Sprache der Mathematik: 
 
Wir müßten die Marinus-Breite mit dem Sekans von 36°, d.i. mit dem Kehrwert des Cosinus von 36° multiplizieren.
Wie würde das für eine Oslo-Karte aussehen?
 
  • Oslo liegt auf der 60°-Breite: cos(60°) = l / 2.
  • Die „klassische" Marinus-Breite ist wieder l.
  • Die Längendistanz ist dafür halbiert worden: Das "wahre Verhältnis" der Oslo-Breite zum Äquator beträgt 0.5.
  • Wir müssen 0.5 mit dem Kehrwert von 1 / 2, d.i. 2 / 1 multiplizieren, um die Oslo-Längendistanz auf Äquatordistanz zu bringen.
  • Indem wir das tun, müssen wir den "klassischen" Abstand zwischen der 60. und der 70. Breite (=1) ebenfalls mit 2 multiplizieren: Der Breitenabstand wird vergrößert und erhält den Wert 2.


Wenn wir die Zusammenhänge ein wenig verallgemeinern, erhalten wir den folgenden Überblick:
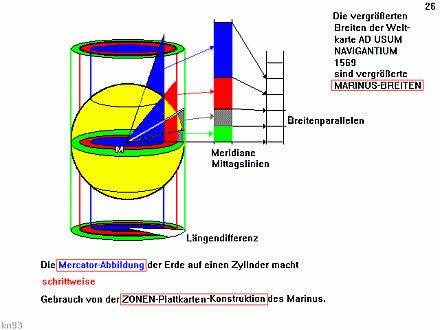Schauen wir uns die Dinge prinzipiell an.
Reduzieren wir die Komplexität, d.h. reduzieren wir den Schnitt auf das Wesentliche:
  • Angenommen wir befinden uns in der Breite j und wollen um den Winkel Dj=a fortschreiten.
Ohne uns etwa nun trigonometrischer Argumente zu bedienen, schließen wir folgendermaßen:
1. Der 4. Lehrsatz im VI. Buche der Elemente von Euklid lautet:
 
In winkelgleichen Dreiecken stehen die Seiten um gleiche Winkel in Proportion, undzwar entsprechen einander die, die gleichen Winkeln gegenüber liegen.
2. Da die beiden Dreiecke MDE und EFG "nahezu" ähnlich sind - der Winkelfehler beträgt gerade einmal a/2 - , gilt in ihnen der Lehrsatz näherunsgweise.

Aus der betreffenden Proportion folgt :
 

  • EG » EF · ( ME / MD ) = Marinus-Breite EF · sec(j)


Damit ist die Lösung konstruktiv erreicht. - Über den Secans brauchen wir uns keine Gedanken zu machen: der Quotient ME / MD reicht völlig aus. -

In den Worten Gerhard Mercators lautet die Lösung:
Da wir den Fehler der Plattkarte bedacht haben,
gradus latitudinum
versus utrumque polum
paulatim auximus
pro incremento parallelorum
supra rationem
quam habent ad aequinoctialem.		 haben wir die Breitengrade [Breitengradabstände EF]
allmählich in dem Maße vergrößert [· (ME/MD)]
wie die Längengradr [Längengradabstände]
in ihrem Verhältnis [MD/ME] zum 
Äquator[abschnitt] zunehmen.
Zu diesen Überlegungen sind allein die Kenntnisse der euklidischen Ähnlichkeitslehre vonnöten: BUCH VI, LEHRSATZ 4.


Wie die Konstruktion der Weltkarte wohl verlaufen ist, das ahnen wir nun schon:

Gerhard Mercator brauchte den Fehler a/2 nur "hinreichend" klein zu machen, z.B. ein halbes Grad groß, um in die Gegend von Zeichenfehlern zu kommen.
Die Rekonstruktion des Baseler Exemplars zeigt:

l°-Schritte bei einem Kreis = Kugelradius von 315 mm unter Anwendung der "Mittelbreitenmethode" der Seeleute führen auf die Weltkarte von 1569 in einer wünschenswerten Übereinstimmung.

Die Zeichenfehler liegen i.a. unter 0.2 mm, die Übereinstimmung der betreffenden Folgen Original : Rekonstruktion beläuft sich auf 0.9997.

Eine Anleitung zur Rekonstruktion des Gradnetzes einer Mercator-Karte in kleinerem Maßstab - man muß ja nicht gleich meine Rekonstruktion mit originalen 315 mmm wiederholen - habe ich vorbereitet.