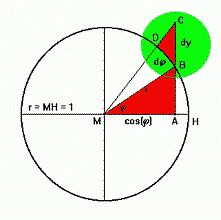
Für Abiturienten und solche, die es werden wollen -
.
d. h. für diejenigen, die schon die Analysis und ihre Methoden kennengelernt haben - läßt sich aus den Marinus-Mercator-Schemata eine Differentialgleichung herauslesen, deren Integration zur "exakten" Lösung der Mercator-Aufgabe führt, die "vergrößerten Breiten" - nun aber nicht zu zeichnen, sondern (hinreichend genau) - zu berechnen. (Wer die Lösung nachschlagen will, der kann die Duisburger Forschungen, Bd. 41, 1994, aufschlagen.)
 Anhand der Figur geht die Proportion Gerhard Mercators über in: dy : dj = l : cos(j) =>; dy = sec(j) · dj, mit sec(j) = l / cos(j).

Integrieren wir über [0 | j], so erhalten wir nach Multiplikation mit R für die Breite Bj die Lösung: 
Bj = R · ln(tan(p / 4 + j / 2)).

Hier einige Tips, wie man vorgehen kann:
(1) Löse cos(2j) = cos²(j) - sin²(j) nach cos(j) auf und substituiere.
(2) Was folgt, wenn Du die Kreisformel sin² + cos² = 1 benutzt?
(3) Erweitere den Quotienten mit 1/cos²(j /2).
(4) Ersetze das resultierende tan-Glied durch a, und löse nach a auf.
(5) Zeige, daß nunmehr dj = 2da/(1+a²).
(6) Mit Hilfe einer Partialbruchzerlegung gelangst Du zu der Formel dj/cos(j ) = da/(1+a) + da/(1-a).
(7) Integration und Resubstitution führen für C=0 auf unsere Formel. [In Browsern ohne Darstellung des griechischen Alfabets: j = phi]